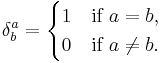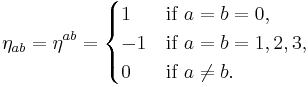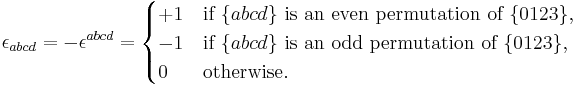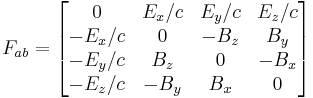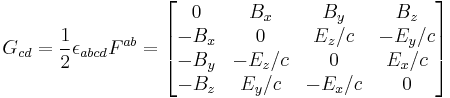Lorentz covariance
In standard physics, Lorentz symmetry is "the feature of nature that says experimental results are independent of the orientation or the boost velocity of the laboratory through space".[1] Lorentz covariance is a related concept, covariance being a measure of how much two variables change together.
Lorentz covariance (from Hendrik Lorentz) is a key property of spacetime that follows from the special theory of relativity. Lorentz covariance has two distinct, but closely related meanings:
- A physical quantity is said to be Lorentz covariant if it transforms under a given representation of the Lorentz group. According to the representation theory of the Lorentz group, these quantities are built out of scalars, four-vectors, four-tensors, and spinors. In particular, a scalar (e.g. the space-time interval) remains the same under Lorentz transformations and is said to be a Lorentz invariant (i.e. they transform under the trivial representation).
- An equation is said to be Lorentz covariant if it can be written in terms of Lorentz covariant quantities (confusingly, some use the term invariant here). The key property of such equations is that if they hold in one inertial frame, then they hold in any inertial frame (this follows from the result that if all the components of a tensor vanish in one frame, they vanish in every frame). This condition is a requirement according to the principle of relativity, i.e. all non-gravitational laws must make the same predictions for identical experiments taking place at the same spacetime event in two different inertial frames of reference.
Note: this usage of the term covariant should not be confused with the related concept of a covariant vector. On manifolds, the words covariant and contravariant refer to how objects transform under general coordinate transformations. Confusingly, both covariant and contravariant four-vectors can be Lorentz covariant quantities.
Local Lorentz covariance, which follows from general relativity, refers to Lorentz covariance applying only locally in an infinitesimal region of spacetime at every point.
There is a generalization of this concept to cover Poincaré covariance and Poincaré invariance.
Contents |
Examples
In general, the nature of a Lorentz tensor can be identified by its tensor rank, which is the number of indices it has. No indices implies it is a scalar, one implies it is a vector etc. Furthermore, any number of new scalars, vectors etc. can be made by contracting any kinds of tensors together, but many of these may not have any real physical meaning. Some of those tensors that do have a physical interpretation are listed (by no means exhaustively) below.
Please note, the metric sign convention such that η = diag (1, −1, −1, −1) is used throughout the article.
Lorentz scalars
Proper time (for timelike intervals):
Electromagnetism invariants:
D'Alembertian/wave operator:
Lorentz 4-vectors
4-Displacement:
Partial derivative:
Lorentz 4-tensors
The Kronecker delta:
The Minkowski metric (the metric of flat space according to General Relativity):
The Levi-Civita symbol:
Electromagnetic field tensor (using a metric signature of + − − − ):
Dual electromagnetic field tensor:
Lorentz violation
Lorentz violation refers to theories which are approximately relativistic when it comes to experiments that have actually been performed (and there are quite a number of such experimental tests) but yet contain tiny or hidden Lorentz violating corrections.
Such models typically fall into four classes:
- The laws of physics are exactly Lorentz covariant but this symmetry is spontaneously broken. In special relativistic theories, this leads to phonons, which are the Goldstone bosons. The phonons travel at less than the speed of light.
- Similar to the approximate Lorentz symmetry of phonons in a lattice (where the speed of sound plays the role of the critical speed), the Lorentz symmetry of special relativity (with the speed of light as the critical speed in vacuum) is only a low-energy limit of the laws of Physics, which involve new phenomena at some fundamental scale. Bare conventional "elementary" particles are not point-like field-theoretical objects at very small distance scales, and a nonzero fundamental length must be taken into account. Lorentz symmetry violation is governed by an energy-dependent parameter which tends to zero as momentum decreases. Such patterns require the existence of a privileged local inertial frame (the "vacuum rest frame"). They can be tested, at least partially, by ultra-high energy cosmic ray experiments like the Pierre Auger Observatory.
- The laws of physics are symmetric under a deformation of the Lorentz or more generally, the Poincaré group, and this deformed symmetry is exact and unbroken. This deformed symmetry is also typically a quantum group symmetry, which is a generalization of a group symmetry. Deformed special relativity is an example of this class of models. It is not accurate to call such models Lorentz-violating as much as Lorentz deformed any more than special relativity can be called a violation of Galilean symmetry rather than a deformation of it. The deformation is scale dependent, meaning that at length scales much larger than the Planck scale, the symmetry looks pretty much like the Poincaré group. Ultra-high energy cosmic ray experiments cannot test such models.
- This is a class of its own; a subgroup of the Lorentz group is sufficient to give us all the standard predictions if CP is an exact symmetry. However, CP isn't exact. This is called Very Special Relativity.
Constraints
In standard field theory, there are very strict and severe constraints on marginal and relevant Lorentz violating operators within both QED and the Standard Model. Irrelevant Lorentz violating operators may be suppressed by a high cutoff scale, but they typically induce marginal and relevant Lorentz violating operators via radiative corrections. So, we also have very strict and severe constraints on irrelevant Lorentz violating operators.
Models belonging to the first two classes can be consistent with experiment if Lorentz breaking happens at Planck scale or beyond it, and if Lorentz symmetry violation is governed by a suitable energy-dependent parameter. One then has a class of models which deviate from Poincaré symmetry near the Planck scale but still flows towards an exact Poincaré group at very large length scales. This is also true for the third class, which is furthermore protected from radiative corrections as one still has an exact (quantum) symmetry.
The Fermi telescope has not found any modification in the dispersion relation for gamma rays up to the level given by the Planck scale.[2]
In September 2011, the OPERA collaboration at CERN indicated detection of muon neutrinos sent 730 kilometers (454 miles) from near Geneva, Switzerland to the Gran Sasso National Laboratory in Italy traveling faster than light by a factor of approximately 1 in 40,000, a statistic with 6.0-sigma significance.[3] (see faster-than-light neutrino anomaly)
CPT violation
In 2002, Oscar Greenberg proved that CPT violation implies the breaking of Lorentz symmetry.[4] Even though there is no evidence of the violation of Lorentz invariance, several experimental searches for such violations have been performed during recent years. A detailed summary of the results of these searches is given in the Data Tables for Lorentz and CPT Violation.[5] Potential violation in high-speed-ion experiments has been shown recently with many criticisms against the interpretation of the analysis done.[6]
See also
- Antimatter tests of Lorentz violation
- Background independence
- Deformed special relativity
- General covariance
- List of mathematical topics in relativity
- Loop quantum gravity
- Hendrik Lorentz
- Lorentz invariance in loop quantum gravity
- Lorentz transformation
- Lorentz-violating neutrino oscillations
- Luminiferous aether
- Pierre Auger Observatory
- Principle of locality
- Relativistic mass
- Rotational symmetry
- Spacetime
- Spin foam
- Standard-Model Extension
- Symmetry in physics
- Test theories of special relativity
- Translational symmetry
References
- ^ http://cerncourier.com/cws/article/cern/29224
- ^ Abdo, A. A.; Ackermann, M.; Ajello, M.; Asano, K.; Atwood, W. B.; Axelsson, M.; Baldini, L.; Ballet, J. et al. (19 Nov 2009). "A limit on the variation of the speed of light arising from quantum gravity effects". Nature 462 (7271): 331–334. Bibcode 2009Natur.462..331A. doi:10.1038/nature08574. PMID 19865083. http://www.nature.com/nature/journal/v462/n7271/full/nature08574.html.
- ^ BBC News - Speed-of-light results under scrutiny at Cern
- ^ Greenberg, O.W. (2002). "CPT Violation Implies Violation of Lorentz Invariance". Physical Review Letters 89 (23): 231602. arXiv:hep-ph/0201258. Bibcode 2002PhRvL..89w1602G. doi:10.1103/PhysRevLett.89.231602.
- ^ Kostelecky, V.A.; Russell, N. (2010). Data Tables for Lorentz and CPT Violation. arXiv:0801.0287v3.
- ^ Devasia, S. (2010). "Lorentz violation in high-energy ions". The European Physical Journal C - Particles and Fields 69 (3-4): 343–346. Bibcode 2010EPJC...69..343D. doi:10.1140/epjc/s10052-010-1437-9.
- Background information on Lorentz and CPT violation: http://www.physics.indiana.edu/~kostelec/faq.html
- http://relativity.livingreviews.org/Articles/lrr-2005-5/
- Amelino-Camelia G, Ellis J, Mavromatos N E, Nanopoulos D V, and Sarkar S (June 1998). "Tests of quantum gravity from observations of bold gamma-ray bursts". Nature 393 (6687): 763–765. arXiv:astro-ph/9712103. Bibcode 1998Natur.393..763A. doi:10.1038/31647. http://www.nature.com/nature/journal/v393/n6687/full/393763a0_fs.html. Retrieved 2007-12-22.
- Jacobson T, Liberati S, and Mattingly D (August 2003). "A strong astrophysical constraint on the violation of special relativity by quantum gravity". Nature 424 (6952): 1019–1021. arXiv:astro-ph/0212190. Bibcode 2003Natur.424.1019J. doi:10.1038/nature01882. PMID 12944959. http://www.nature.com/nature/journal/v424/n6952/full/nature01882.html. Retrieved 2007-12-22.
- Carroll S (August 2003). "Quantum gravity: An astrophysical constraint". Nature 424 (6952): 1007–1008. Bibcode 2003Natur.424.1007C. doi:10.1038/4241007a. PMID 12944951. http://www.nature.com/nature/journal/v424/n6952/full/4241007a.html. Retrieved 2007-12-22.
- http://scitation.aip.org/getabs/servlet/GetabsServlet?prog=normal&id=PRVDAQ000067000012124011000001
- Gonzalez-Mestres, L., "Lorentz symmetry violation and the results of the AUGER experiment", http://arxiv.org/abs/0802.2536
- Fermi GBM/LAT Collaborations, "Testing Einstein's special relativity with Fermi's short hard gamma-ray burst GRB090510", http://arxiv.org/abs/0908.1832
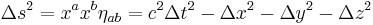
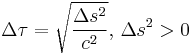
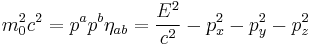
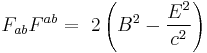
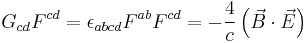
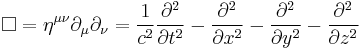
![x^a = \left[ct, x, y, z\right]](/2012-wikipedia_en_all_nopic_01_2012/I/2ada7d697041b579bc72c6ff27d61cc9.png)
![\partial_a = \left[ \frac{1}{c}\frac{\partial}{\partial t}, \frac{\partial}{\partial x}, \frac{\partial}{\partial y}, \frac{\partial}{\partial z} \right]](/2012-wikipedia_en_all_nopic_01_2012/I/bb8f337e20562403a959a637acaedb63.png)
![U^a = \frac{dx^a}{d\tau} = \gamma \left[c, \frac{dx}{dt}, \frac{dy}{dt}, \frac{dz}{dt}\right]](/2012-wikipedia_en_all_nopic_01_2012/I/747183479e965c47c803fa16e69c26e6.png)
![p^a = m_0 U^a = \left[\frac{E}{c}, p_x, p_y, p_z\right]](/2012-wikipedia_en_all_nopic_01_2012/I/69f01d0c078685664ed6d9e1dfae9ee1.png)
![j^a = \left[c\rho, j_x, j_y, j_z\right]](/2012-wikipedia_en_all_nopic_01_2012/I/176e78c5678b6ef4a78af6d0c83650c7.png)